|
| | Blog Taamer |  |
|
+4Chrismir Seb-007 prop38 Taamer 8 participants | |
| Auteur | Message |
|---|
Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 16:06 Ven 19 Fév 2010 - 16:06 | |
| - M@jK a écrit:
- Whaou tu m'as fait mal à la tête avec ton post !
Je ne comprends rien à ton raisonnement, voilà ce que j'ai cru comprendre :
Tu cherche à calculer le nombre de permutations qui ne laissent aucune cartes à la même place, en supposant que les deux jeux de départ soient rangés de manière identiques (jeux neufs ?) et tu en déduis la probabilité d'avoir une collision ?
Si j'ai bien compris le problème est :
"quelle est la probabilité d'avoir au moins une collision entre deux permutations aléatoires de S_52 ?"
Concernant ton post je me permet quelques remarques :
- dans le paragraphe calcul de A(i) il n'est pas utile d'introduire une variable n puisque n est constant et égal à 52
- dans ce même paragraphe, A(i) n'est pas égal à 52!/i! (suffit de prendre i=1 pour s'en convaincre) En fait A(i) n'est pas égal à C(52,i)*(52-i)!
Quand tu dis :
"on choisit i cartes parmi 52, cela vaut C(52,i), puis on dispose les (n-i) cartes restantes par n'importe quel mélange, ce qui vaut (n-i)!."
Ce n'est justement pas n'importe quel mélange sinon tu comptes plusieurs fois les mêmes mélanges.
Exemples avec 4 cartes {1,2,3,4}
Je fixe 2, je compte donc le mélange {4,2,3,1} qui laisse 2 à la même place
Je fixe 3, je compte donc le mélange {4,2,3,1} qui laisse 3 à la même place.
Du coup {4,2,3,1} a été compté deux fois....
Bref Si j'ai le temps je réfléchirai au problème, mais ça ne me semble pas si simple... En fait tout est juste, mais il y a quelques précisions que je n'ai pas indiquées - ceci dit, tu as mis le doigt dessus. Dans l'exemple des formes/couleurs, quand on compte A(1)=3 verts + 2 chats, on compte deux fois le chat vert (propriété chat et propriété vert). C'est le fait qu'on compte parfois plusieurs fois un même élément (et qu'on le rajoute dans A(1) et qu'on l'enlève dans A(2)) qui fait qu'on retombe sur nos pieds à la fin. Et ce qui fait que ça s'appelle "inclusion-exclusion". Ceci explique que A(i), pris tout seul, ne corresponde à rien. La notion que notre cerveau manipule plus facilement, c'est B(i) : si j'appelle B(i) le nombre d'éléments qui ont exactement i propriétés, alors on a une relation qui ressemble à A(1)=B(1)+2*B(2)+3*B(3) etc. En plus, les coefficients ne sont pas linéaires, mais combinatoires / arithmétiques / pascaliens (1, 2, 3, 6, 10, etc.) Ce qui t'est venu naturellement à l'esprit, c'est que "B(1)=A(1) - des éléments qu'on a comptés en trop". C'est tout à fait exact, sauf que la formule finale est puissante quand on manipule A(i), mais pas B(i). - M@jK a écrit:
"Tu cherche à calculer le nombre de permutations qui ne laissent aucune cartes à la même place, en supposant que les deux jeux de départ soient rangés de manière identiques (jeux neufs ?) et tu en déduis la probabilité d'avoir une collision ?" --> là tu écris une connerie, que les deux jeux au départ soient rangés de la même manière n'a aucune importance, tout simplement parce que les permutations forment un groupe, et donc une permutation d'une permutation est encore une permutation, avec la même probabilité d'être un dérangement (ou de ne pas l'être, il suffit de remplacer f par gof et tout est pareil). Pour t'en convaincre, dis-toi que le jeu de ton copain donne l'ordre de référence (aléatoire, puisqu'il a été battu), mais que rien n'oblige que l'ordre de référence soit 1, 2, 3, .., 52. Je pourrai te donner d'autres références sur le même sujet (inclusion-exclusion, et le coup des cartes), qui te donneront la même chose expliquée autrement. L'intérêt majeur du calcul de A(1), A(2) etc., c'est d'avoir à fixer les conditions minimales pour que ce soit bon, et après à ne pas avoir à dénombrer les cas particuliers "que l'on compte plusieurs fois". La formule fera le ménage pour toi à la fin, d'où sa puissance dans des problèmes de dénombrements combinatoires parfois compliqués. P.S. En effet, je n'ai pas besoin de n, qui vaut 52 dans l'exemple. Je me suis posé tout seul la question de savoir "combien de cartes dans le paquet faut-il pour que le jeu soit "intéressant"", et là aussi, la réponse est déjà écrite (en filigrane) dans mon blog, en décortiquant la formule finale (la somme partielle converge très, très vite vers 1/e). A n=2, le jeu est à 50-50; dès que n=3, le jeu est favorable à la collision (comme tu dis). | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 16:14 Ven 19 Fév 2010 - 16:14 | |
| Dans l'exemple avec les nombres que 2 divise ou que 3 divise, tous les multiples de 6 sont comptés deux fois dans A(1) (qui vaut 50+33=83), et A(2) enlève les doublons dans la formule finale.
C'est le truc pour comprendre et utiliser cette formule.
Edit : blog corrigé, n a été remplacé par 52 dans le dernier exemple. | |
|   | | Chrismir
Bragger Professionnel


Nombre de messages : 3319
Age : 42
Localisation : Froges
Emploi : Poker Player
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 16:19 Ven 19 Fév 2010 - 16:19 | |
| - Taamer a écrit:
- M@jK a écrit:
- Whaou tu m'as fait mal à la tête avec ton post !
Je ne comprends rien à ton raisonnement, voilà ce que j'ai cru comprendre :
Tu cherche à calculer le nombre de permutations qui ne laissent aucune cartes à la même place, en supposant que les deux jeux de départ soient rangés de manière identiques (jeux neufs ?) et tu en déduis la probabilité d'avoir une collision ?
Si j'ai bien compris le problème est :
"quelle est la probabilité d'avoir au moins une collision entre deux permutations aléatoires de S_52 ?"
Concernant ton post je me permet quelques remarques :
- dans le paragraphe calcul de A(i) il n'est pas utile d'introduire une variable n puisque n est constant et égal à 52
- dans ce même paragraphe, A(i) n'est pas égal à 52!/i! (suffit de prendre i=1 pour s'en convaincre) En fait A(i) n'est pas égal à C(52,i)*(52-i)!
Quand tu dis :
"on choisit i cartes parmi 52, cela vaut C(52,i), puis on dispose les (n-i) cartes restantes par n'importe quel mélange, ce qui vaut (n-i)!."
Ce n'est justement pas n'importe quel mélange sinon tu comptes plusieurs fois les mêmes mélanges.
Exemples avec 4 cartes {1,2,3,4}
Je fixe 2, je compte donc le mélange {4,2,3,1} qui laisse 2 à la même place
Je fixe 3, je compte donc le mélange {4,2,3,1} qui laisse 3 à la même place.
Du coup {4,2,3,1} a été compté deux fois....
Bref Si j'ai le temps je réfléchirai au problème, mais ça ne me semble pas si simple...
En fait tout est juste, mais il y a quelques précisions que je n'ai pas indiquées - ceci dit, tu as mis le doigt dessus.
Dans l'exemple des formes/couleurs, quand on compte A(1)=3 verts + 2 chats, on compte deux fois le chat vert (propriété chat et propriété vert). C'est le fait qu'on compte parfois plusieurs fois un même élément (et qu'on le rajoute dans A(1) et qu'on l'enlève dans A(2)) qui fait qu'on retombe sur nos pieds à la fin. Et ce qui fait que ça s'appelle "inclusion-exclusion".
Ceci explique que A(i), pris tout seul, ne corresponde à rien. La notion que notre cerveau manipule plus facilement, c'est B(i) : si j'appelle B(i) le nombre d'éléments qui ont exactement i propriétés, alors on a une relation qui ressemble à A(1)=B(1)+2*B(2)+3*B(3) etc.
En plus, les coefficients ne sont pas linéaires, mais combinatoires / arithmétiques / pascaliens (1, 2, 3, 6, 10, etc.)
Ce qui t'est venu naturellement à l'esprit, c'est que "B(1)=A(1) - des éléments qu'on a comptés en trop". C'est tout à fait exact, sauf que la formule finale est puissante quand on manipule A(i), mais pas B(i).
- M@jK a écrit:
"Tu cherche à calculer le nombre de permutations qui ne laissent aucune cartes à la même place, en supposant que les deux jeux de départ soient rangés de manière identiques (jeux neufs ?) et tu en déduis la probabilité d'avoir une collision ?" --> là tu écris une connerie, que les deux jeux au départ soient rangés de la même manière n'a aucune importance, tout simplement parce que les permutations forment un groupe, et donc une permutation d'une permutation est encore une permutation, avec la même probabilité d'être un dérangement (ou de ne pas l'être, il suffit de remplacer f par gof et tout est pareil).
Pour t'en convaincre, dis-toi que le jeu de ton copain donne l'ordre de référence (aléatoire, puisqu'il a été battu), mais que rien n'oblige que l'ordre de référence soit 1, 2, 3, .., 52.
Je pourrai te donner d'autres références sur le même sujet (inclusion-exclusion, et le coup des cartes), qui te donneront la même chose expliquée autrement.
L'intérêt majeur du calcul de A(1), A(2) etc., c'est d'avoir à fixer les conditions minimales pour que ce soit bon, et après à ne pas avoir à dénombrer les cas particuliers "que l'on compte plusieurs fois". La formule fera le ménage pour toi à la fin, d'où sa puissance dans des problèmes de dénombrements combinatoires parfois compliqués.
P.S. En effet, je n'ai pas besoin de n, qui vaut 52 dans l'exemple. Je me suis posé tout seul la question de savoir "combien de cartes dans le paquet faut-il pour que le jeu soit "intéressant"", et là aussi, la réponse est déjà écrite (en filigrane) dans mon blog, en décortiquant la formule finale (la somme partielle converge très, très vite vers 1/e). A n=2, le jeu est à 50-50; dès que n=3, le jeu est favorable à la collision (comme tu dis). C'est donc ca les fameux nosebleed du poker...  | |
|   | | vieto
Shark Attack !


Nombre de messages : 1708
Age : 45
Localisation : Las Vegas
Emploi : Poker Player
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 16:24 Ven 19 Fév 2010 - 16:24 | |
| J'ai mal.  J'ai beau être matinal (sic), j'ai mal. | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 16:31 Ven 19 Fév 2010 - 16:31 | |
| - Chrismir a écrit:
- C'est donc ca les fameux nosebleed du poker...
 Ouaip, la matrice a un biais du fait que les calculs sont faits comme s'il y avait retirage; la v2 avec le vrai calcul où tout est corrélé sera bientôt prête et je pourrai alors publier. En outre, comme mon prochain article de poker va parler de semi-deals, de "!" et de "!!" (en tant qu'opérateurs mathématiques), il fallait que je commence par un truc un peu soft (si si m@jk c'est soft tout ça), avant de rentrer dans le vif du sujet. La distribution des bourre-pifs a commencé  | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 | |   | | M@jK
Bullets Every Hand


Nombre de messages : 607
Age : 41
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 16:46 Ven 19 Fév 2010 - 16:46 | |
| - Taamer a écrit:
- M@jK a écrit:
"Tu cherche à calculer le nombre de permutations qui ne laissent aucune cartes à la même place, en supposant que les deux jeux de départ soient rangés de manière identiques (jeux neufs ?) et tu en déduis la probabilité d'avoir une collision ?" --> là tu écris une connerie, que les deux jeux au départ soient rangés de la même manière n'a aucune importance J'ai écrits cela car je croyais que tu suivais ce raisonnement, je cherchais à comprendre le cheminement que tu as fait pour établir : "nb de permutations vérifiant les hypothèses" = "nb de dérangements" (ce qui n'est pas très clair à la première lecture) Pour l'écrire de manière plus intuitive et accessible, j'aurais dit ça : "Une fois le premier jeu mélangé, mélanger le deuxième jeu et ne pas avoir de collision est équivalent à re-mélanger le premier et obtenir un dérangement (certes pas très clair non plus)" Du coup je fais le lien avec la formule (merci wikipedia) mais pour que ce soit rigoureux et compréhensible à la première lecture n'écrit pas ça ! "A(i) : le nombre de mélanges qui laisse au moins i cartes fixes se compte ainsi : on choisit i cartes parmi 52, cela vaut C(52,i), puis on dispose les (52-i) cartes restantes par n'importe quel mélange, ce qui vaut (52-i)!. Grâce à l'expression factorielle de C(52,i), le produit des deux simplifie l'expression : A(i) = C(52,i)*(52-i)! = [52!/i!(52-i)!]*(52-i)! = 52!/i!" | |
|   | | M@jK
Bullets Every Hand


Nombre de messages : 607
Age : 41
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 16:53 Ven 19 Fév 2010 - 16:53 | |
| - Taamer a écrit:
- (si si m@jk c'est soft tout ça)
Le plus dur n'est pas de comprendre mais de se faire comprendre  | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 17:05 Ven 19 Fév 2010 - 17:05 | |
| - M@jK a écrit:
- Taamer a écrit:
- (si si m@jk c'est soft tout ça)
Le plus dur n'est pas de comprendre mais de se faire comprendre  En effet, mon explication est à reformuler à partir de là : "Nous allons compter le nombre de mélanges qui laissent au moins une carte en place (A(1)), au moins deux cartes en place (A(2)), etc. jusqu'à toutes les cartes à la même place (A(52)).". Faut pas parler de B pour calculer A, avec les notations de notre discussion. Edit : article remanié; ça ne le rend pas plus compréhensible, mais au moins je n'écris pas de sottises qui vous fichent le doute ou vous mettent dans l'erreur.
Dernière édition par Taamer le Ven 19 Fév 2010 - 17:34, édité 2 fois | |
|   | | M@jK
Bullets Every Hand


Nombre de messages : 607
Age : 41
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 17:16 Ven 19 Fév 2010 - 17:16 | |
| Je dirais :
A(i) = la somme sur 0<j_1<...<j_i<53 du nombre de permutations qui laisse j_1,...,j_i à la même place
Pour A(1) c'est la somme pour i allant de 1 à 52 du nombre de permutations qui laisse i à la même place =51! * 52 = 52!
Bref c'est tendu surtout sur un blog... | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 17:19 Ven 19 Fév 2010 - 17:19 | |
| - M@jK a écrit:
- Je dirais :
A(i) = la somme sur 0<j_1<...<j_i<53 du nombre de permutations qui laisse j_1,...,j_i à la même place
Pour A(1) c'est la somme pour i allant de 1 à 52 du nombre de permutations qui laisse i à la même place =51! * 52 = 52!
Bref c'est tendu surtout sur un blog... ça n'explique pas les termes qu'on compte plusieurs fois? Je vais peut-être écrire un § de type #(AUB)=#A+#B-#(A inter B), ou la version à trois ensembles #(AUBUC)=#A+#B+#C-(#(A inter B)+#(B inter C)+#(C inter A))+#(A inter B inter C). | |
|   | | M@jK
Bullets Every Hand


Nombre de messages : 607
Age : 41
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 17:26 Ven 19 Fév 2010 - 17:26 | |
| La version ensembliste est en effet plus facile à comprendre mais bof bof sur un blog en mode AnB, AuB...(j'ai cru lire quelque part que tu utilises latex, fais des pdf pour les démos au pire)
Dans l'immédiat j'ai quelques trucs à faire mais si la prochaine fois tu as besoin d'une relecture je prendrais volontiers un peu de temps. | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 19 Fév 2010 - 17:33 Ven 19 Fév 2010 - 17:33 | |
| - M@jK a écrit:
- La version ensembliste est en effet plus facile à comprendre mais bof bof sur un blog en mode AnB, AuB...(j'ai cru lire quelque part que tu utilises latex, fais des pdf pour les démos au pire)
J'ai fait du Latex étudiant, mais plus aujourd'hui. J'ai testé l'éditeur de formule de Write, quand tu sauves le document en hacheteumeuleu, il crée automatiquement une image de la formule. J'avais déjà expérimenté (avec l'article sur le rétroclassement) la difficulté de faire passer un article théorique ou calculatoire sur un blog. Merci pour ton offre de relecture. | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Lun 22 Mar 2010 - 17:57 Lun 22 Mar 2010 - 17:57 | |
| Update blog, pas de maths, que du brag accessible à tous (BR up to $132). | |
|   | | Chrismir
Bragger Professionnel


Nombre de messages : 3319
Age : 42
Localisation : Froges
Emploi : Poker Player
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Lun 22 Mar 2010 - 19:02 Lun 22 Mar 2010 - 19:02 | |
| - Taamer a écrit:
J'ai fait du Latex étudiant, mais plus aujourd'hui. Pour les néophyte : - Spoiler:
| |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 12 Nov 2010 - 13:37 Ven 12 Nov 2010 - 13:37 | |
| Update blog. "Froid de novembre, cache ton membre", disait Theillard de Chardin. (Pierre Desproges). | |
|   | | Chrismir
Bragger Professionnel


Nombre de messages : 3319
Age : 42
Localisation : Froges
Emploi : Poker Player
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 12 Nov 2010 - 17:39 Ven 12 Nov 2010 - 17:39 | |
| Lu,
pas tout compris pour le run it twice...
Je suis d'accord sur la 1ere partie ; que la variance est un allié du bon joueur de poker et les arguments associés, avec aussi les contre-arguments potentiels liés à la dynamique de la table (ie le joueur hit'n'run), plus certaines considérations psychologique (tilt ou tilt positif), et le fait de jouer deep si l'un double up et reste.
Mais dans l'histoire du pot 3 way protégé par un short à tapîs avec un jeu faible, je vois pas en quoi le run it twice va l'aider à le bust (techniquement il à même plus de chance de rester avec 1/2 du pot sur un run it twice, que s'il prend le pot total sur un run it once ou au moins il triple et est moins short) donc il me semble qu'il vaudrais mieux run it once dans ce cas là.
Pour le coup en freeroll j'ai pas capté l'histoire de "l’intérêt de faire croître géométriquement le pot et de tirer deux fois", que tu tires deux fois ou une fois ton EV est là même, dans un cas tu vas ship le pot 1/4 du temps, et dans l'autre cas tu vas ship le 1/2 pot 2 fois 1/8eme du temps (on propose le run it twice quand on est à tapis non ? donc techniquement on ne peux plus faire gonfler le pot)
A moins qu'il y ai un truc qui m'échappe...
Sinon il parait que le Omaha (le classique) va être légalisé dans les casino français.
Dernière édition par Chrismir le Ven 12 Nov 2010 - 17:53, édité 1 fois | |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 12 Nov 2010 - 17:50 Ven 12 Nov 2010 - 17:50 | |
| - Chrismir a écrit:
- Lu,
pas tout compris pour le run it twice...
Je suis d'accord sur la 1ere partie ; que la variance est un allié du bon joueur de poker et les arguments associés, avec aussi les contre-arguments potentiels liés à la dynamique de la table (ie le joueur hit'n'run), plus certaines considérations psychologique (tilt ou tilt positif), et le fait de jouer deep si l'un double up et reste.
Mais dans l'histoire du pot 3 way protégé par un short à tapîs avec un jeu faible, je vois pas en quoi le run it twice va l'aider à le bust (techniquement il à même plus de chance de rester avec 1/2 du pot sur un run it twice, que s'il prend le pot total sur un run it once ou au moins il triple et est moins short) donc vaudrais mieux run it once dans ce cas là.
Pour le coup en freeroll j'ai pas capté l'histoire de "l’intérêt de faire croître géométriquement le pot et de tirer deux fois", que tu tires deux fois ou une fois ton EV est là même, dans un cas tu vas ship le pot 1/4 du temps, et dans l'autre cas tu vas ship le 1/2 pot 2 fois 1/8eme du temps.
A moins qu'il y ai un truc qui m'échappe...
Sinon il parait que le Omaha (le classique) va être légalisé dans les casino français. Run it twice --> à l'ACF aux grosses tables, tu peux te la péter comme sur HSP en tirant deux tableaux (soit turn + river deux fois, soit river deux fois - il faut être à tapis obv). Dans le pot 3-way, souvent un shortstack sera tapis OU commit depuis le préflop, dans ce cas-là tu oublies qu'il est là parce que sa main a peu de chances de connecter avec le flop (sachant que vous êtes déjà deux joueurs intéressés par ce flop). Pour le freeroll, s'il y a 240 au pot et un flop 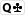 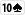  , le mec potte devant toi (240) avec KJxxx, et toi tu vas repotter (960) parce que tu as mieux (par exemple AKJQQ :-p~~). En gros le mec sait qu'il est max pour l'instant, mais il doit ajouter 720 pour défendre 120 (sa demi-part du pot), et peut-être plus s'il reste de l'argent à miser derrière. Ici, la rareté du freeroll (où ton adversaire n'a AUCUNE chance complémentaire de gagner tout seul) fait qu'on peut choisir de limiter la variance (loi de Poisson et non plus Gaussienne-like) en tirant deux fois, pour avoir plus de chances de faire 3/4-1/4. Bien sûr, en équité ça ne change rien. Pour l'Omaha en casino il me semble avoir lu des topics sur le sujet (rake 2%), mais je n'ai pas vérifié si le décret d'application avait été publié. | |
|   | | Chrismir
Bragger Professionnel


Nombre de messages : 3319
Age : 42
Localisation : Froges
Emploi : Poker Player
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Ven 12 Nov 2010 - 18:12 Ven 12 Nov 2010 - 18:12 | |
| En parlant de freeroll (je met un spoiler pour pas trop poluer le topic) : - Spoiler:
$1/$2 No Limit Holdem OnGame 6 Players Stacks:UTG ( $211.40) UTG+1 ( $208.10) CO ( $206.10) BTN ( $232.70) SB ($199.90) Hero ($217.60) Pre-Flop: ( $3, 6 players) Hero is BB  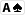 4 folds 4 folds, SB raises to $8, Hero calls $6 Flop: 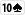  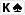 ( $16, 2 players) SB bets $10, Hero calls $10 Turn:  ( $36, 2 players) SB checks, Hero bets $199.60, SB calls $181.90 River:  ( $417.50, 2 players) Final Pot: $417.50SB shows   Hero shows  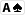 Hero collects $216.10 (net -$1.50) SB collects $198.40 (net -$1.50) Vilain est dans la team alpha (clairement le moins bon de la team d'ailleurs AMHA) et fait des vidéos pour les limpers, belle table d'ailleurs car il y a kastet (meilleur reg du moment sur ongame) et vieto présent aussi. Le play de héro est il ok compte tenu de la range de vilain et ses réactions attendues ? Le call de vilain est il ok ? (ne pas répondre, on va pas pourrir le topic d'Alex)
| |
|   | | Taamer
Shark Attack !


Nombre de messages : 3672
Age : 49
Localisation : Saint Martin d'Uriage
Emploi : Dell Powervault Equallogic Compellent
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  Dim 9 Jan 2011 - 1:36 Dim 9 Jan 2011 - 1:36 | |
| Blog mis à jour : bilan fin décembre, et première semaine 2011. Bonne lecture. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Blog Taamer Sujet: Re: Blog Taamer  | |
| |
|   | | | | Blog Taamer |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
